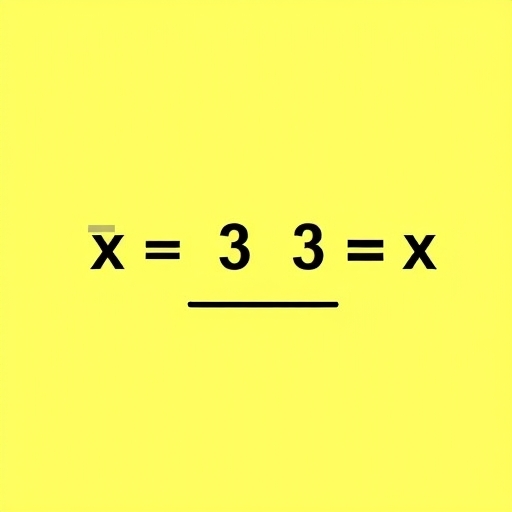How to Find Square Root Without a Calculator
Finding the square root of a number is a fundamental mathematical concept that can be useful in various fields such as engineering, physics, finance, and everyday problem-solving. While calculators make this task easy, understanding how to find the square root manually can enhance your mathematical skills and boost your confidence. In this article, we will explore several methods to find square roots without a calculator, including the prime factorization method, the long division method, and estimation techniques.
Understanding Square Roots
Before diving into the methods, it’s essential to understand what a square root is. The square root of a number ( n ) is a value ( x ) such that ( x^2 = n ). In simpler terms, if you multiply ( x ) by itself, you should get ( n ). For example, the square root of 25 is 5, because ( 5 times 5 = 25 ).
Key Terms
- Perfect Square: A number that has an integer as its square root (e.g., 1, 4, 9, 16, 25).
- Non-Perfect Square: A number that does not have an integer as its square root (e.g., 2, 3, 5, 7).
Methods to Find Square Roots
1. Prime Factorization Method
The prime factorization method involves breaking down a number into its prime factors. This method is particularly useful for perfect squares.
Steps:
1. Find the prime factors of the number.
2. Pair the prime factors: For every two identical prime factors, take one out of the square root.
3. Multiply the paired factors together to find the square root.
Example: Finding the Square Root of 36
1. Prime Factorization: ( 36 = 2 times 2 times 3 times 3 ) or ( 2^2 times 3^2 ).
2. Pair the Factors: ( (2^2) ) and ( (3^2) ).
3. Take one from each pair: ( 2 ) and ( 3 ).
4. Multiply: ( 2 times 3 = 6 ).
Thus, the square root of 36 is 6.
2. Long Division Method
The long division method for square roots is a systematic approach that can be used for both perfect and non-perfect squares.
Steps:
1. Group the digits of the number into pairs, starting from the decimal point and moving left and right.
2. Find the largest integer whose square is less than or equal to the leftmost group.
3. Subtract the square of this integer from the leftmost group and bring down the next pair.
4. Double the divisor and find a digit to append, such that the new number multiplied by the digit is less than or equal to the current dividend.
5. Repeat the process for more decimal places as needed.
Example: Finding the Square Root of 50
1. Group the Digits: 50 can be grouped as (50). Since it has no decimal, we can consider it as 50.00.
2. Find the Largest Integer: The largest integer whose square is less than 50 is 7 (since ( 7^2 = 49 )).
3. Subtract and Bring Down: ( 50 – 49 = 1 ). Bring down the next pair (00), making it 100.
4. Double the Divisor: ( 7 times 2 = 14 ). Find a digit ( x ) such that ( 14x times x leq 100 ). Here, ( x = 7 ) works since ( 147 times 7 = 1029 ) is too high, but ( 146 times 6 = 876 ) is valid.
5. Continue: Repeat this for more precision if necessary.
Thus, the approximate square root of 50 is around 7.07.
3. Estimation Method
For quick calculations, estimation is a handy technique. This method is best for non-perfect squares where you can find two perfect squares between which the number lies.
Steps:
1. Identify the two perfect squares between which your number lies.
2. Estimate: Take the average or a number closer to the perfect square that is lower.
Example: Finding the Square Root of 20
1. The perfect squares near 20 are ( 16 (4^2) ) and ( 25 (5^2) ).
2. Since ( 20 ) is closer to ( 16 ), we can estimate the square root to be slightly more than ( 4 ).
3. A better estimate could be ( 4.5 ) since ( 4.5^2 = 20.25 ), which is close enough.
4. Using the Babylonian Method (Heron’s Method)
The Babylonian method is an ancient technique for estimating square roots that involves averaging.
Steps:
1. Make an initial guess for the square root.
2. Divide the number by the guess.
3. Average the result with the guess to get a new guess.
4. Repeat until the desired precision is achieved.
Example: Finding the Square Root of 10
1. Initial guess: ( 3 ) (since ( 3^2 = 9 )).
2. Divide: ( 10 / 3 approx 3.33 ).
3. Average: ( (3 + 3.33) / 2 approx 3.17 ).
4. Repeat: Now divide ( 10 / 3.17 approx 3.15 ) and average again.
After a few iterations, you will converge to approximately ( 3.16 ).
Comparison of Methods
| Method | Best For | Pros | Cons |
|---|---|---|---|
| Prime Factorization | Perfect Squares | Simple for small numbers, clear process | Not efficient for large numbers |
| Long Division | Any number | Accurate for both perfect and non-perfect | Requires more steps, can be tedious |
| Estimation | Quick estimates | Fast and practical for rough calculations | Less precise |
| Babylonian Method | Any number | Fast convergence, easy to use | Requires initial guess |
FAQ
What is a perfect square?
A perfect square is a number that can be expressed as the square of an integer. For example, ( 1, 4, 9, 16, ) and ( 25 ) are perfect squares.
Can I find square roots of negative numbers?
No, square roots of negative numbers are not defined in the real number system. However, they can be represented in the complex number system using the imaginary unit ( i ).
Why is finding the square root important?
Finding the square root is essential in various fields, including geometry, algebra, and real-world applications such as calculating areas, solving quadratic equations, and understanding statistical measures.
How accurate can I get with these methods?
The accuracy of these methods depends on how many iterations you perform (in the case of the Babylonian method) or how detailed your long division is. With enough precision, you can achieve a very accurate square root.
Conclusion
Finding the square root without a calculator can be a rewarding experience, enhancing your mathematical understanding and problem-solving skills. Whether using the prime factorization method, long division, estimation, or the Babylonian method, each technique has its advantages and is suited to different types of numbers. By practicing these methods, you can become proficient in calculating square roots, preparing you for more advanced mathematical concepts in the future.